Formele de unda dreptunghiulare
Formele de unda dreptunghiulare sunt echivalente unei forme de unda sinusoidala de aceeasi frecventa (fundamentala) insumata cu o serie infinita de unde sinusoidale (armonici) de frecvente multiplu impar ale fundamentalei.
Orice forma de unda periodica, ne-sinusoidala poate fi reprezentata ca serie de semnale sinusoidale de frecvente si amplitudini diferite insumate impreuna.
Definitia semnalului dreptunghiular
Este cunoscut faptul ca orice semnal periodic (ce se repeta in timp) ne-sinusoidal poate fi reprezentat ca si combinatie de semnale continue, sinusoidale si/sau cosinusoidale (semnal sinusoidal defazat cu 90 de grade) de frecvente si amplitudini variate. Acest lucru este perfect valabil indiferent cat de „ciudat” sau „contorsionat” ar parea semnalul analizat. Intr-un caz particular, formele de unda dreptunghiulare sunt echivalente din punct de vedere matematic cu suma unui semnal sinusoidal fundamental, de o anumita frecventa, plus o serie infinita de multiplii impari ai frecventei fundamentale cu amplitudini descrescatoare.
Exemplu
Acest adevar, perfect demonstrabil, al formelor de unda pare greu de crezut. Totusi, daca o forma de unda dreptunghiulara este de fapt o serie infinita de armonici sinusoidale adunate impreuna, ar trebui sa putem demonstra acest lucru insumand cateva armonici sinusoidale si obtinand o aproximare a semanlului dreptunghiular. Vom incerca sa facem acest lucru in continuare.
Circuitul considerat consta din cinci surse de tensiune, de amplitudini si frecvente diferite, conectate in serie. Armonicele considerate sunt: cea fundamentala (prima) la o frecventa de 50 Hz, armonica a 3-a (3×50=150Hz), a 5-a, a 7-a si a 9-a (9×50=450Hz). Amplitudinile semnalelor nu sunt nici ele aleatoare, ci, constau din fractia 4/π inmultita cu fractiile 1(4/πx1=4/πV), 1/3, 1/5, 1/7 si 1/9 (4/πx1/9=4/9πV), in functie de armonica corespunzatoare.
Frecventa fundamentala
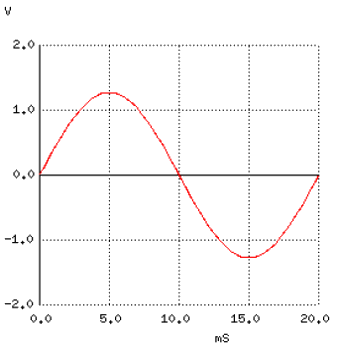
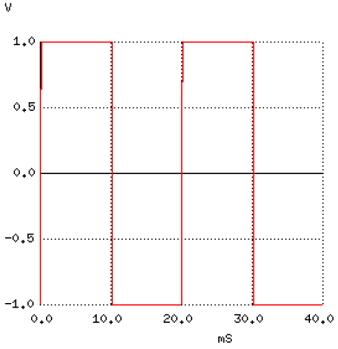
Primul grafic reprezinta tocmai frecventa fundamentala, la 50 Hz si amplitudine de 4/π, adica aproximativ 1.27 V.
Armonica a 3-a
In urmatorul grafic, vom vedea ce se intampla cu acest semnal sinusoidal pur atunci cand il combinam cu armonica a 3-a (150 Hz). Din acest moment, nu mai seamana cu un semnal sinusoidal pur ( semnalul combinat este cel cu rosu). Panta formei de unda la intersectia cu axa orizontala a timpului este mult mai mare acum, semn ca forma de unda initiala se apropie de cea dreptunghiulara.
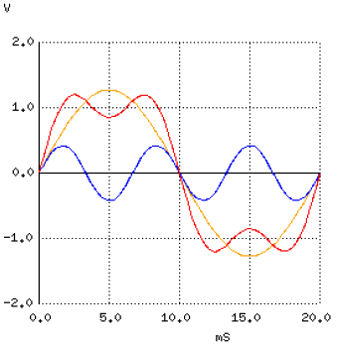
Armonica a 5-a
Sa adaugam in continuare si armonica a 5-a pe grafic. Armonica a 5-a (250 Hz) este reprezentata pe graficul alaturat cu albastru, iar efectele combinate a celor doua armonici sunt reprezentate cu rosu.
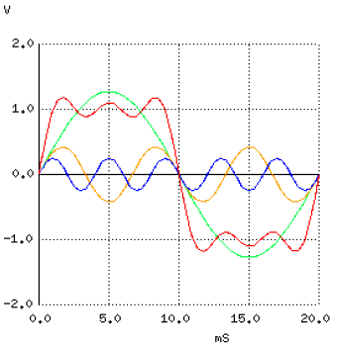
Putem observa cum varful formei de unda s-a aplatizat fata de situatia initiala, iar panta a crescut si mai mult fata de cazul precedent.
Armonica a 7-a si a 9-a
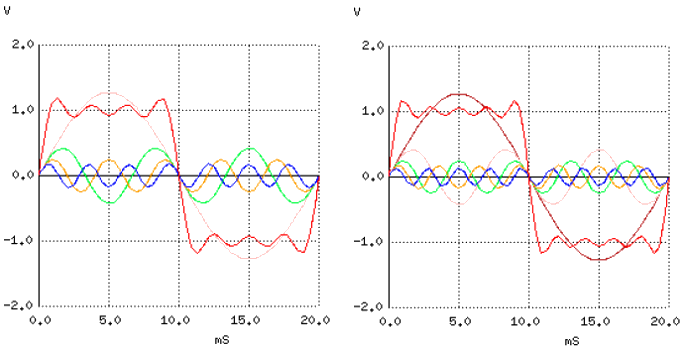
Efectele asupra circuitelor
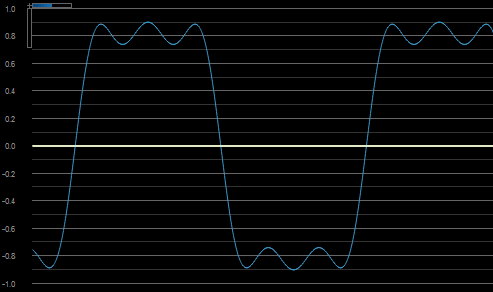
Rezultatul insumarii celor 5 armonici, cu amplitudinile de rigoare, reprezinta o aproximare destul de buna a unui semnal dreptunghiular. Scopul acestui exemplu a fost ilustrarea modului de construire a unui semnal dreptunghiular folosind semnale sinusoidale multiple la frecvente diferite pentru a demonstra faptul ca un semnal pur dreptunghiular este intr-adevar echivalent cu o serie de semnale sinusoidale.
Atunci cand se aplica un semnal dreptunghiular intr-un circuit ce contine elemente reactive (condensatoare si/sau bobine), acele componente se comporta ca si cum am fi aplicat mai multe tensiuni de frecvente diferite in acelasi timp, ceea ce de fapt am si facut.
Analiza Fourier
Faptul ca semnalele ne-sinusoidale periodice sunt echivalente cu o serie de semnale de curent continuu, sinusoidale si/sau cosinusoidale este o consecinta intrinseca a modului de „functionare” al semnalelor: o proprietate fundamentala a tuturor formelor de unda, indiferent ca sunt electrice sau mecanice.
Procesul matematic de reducere a acestor forme de unda nesinusoidale ca suma a componentelor sale la frecvente si amplitudini diferite, poarta numele de analiza Fourier, fiind un proces destul de complicat. Analiza Fourier este in schimb usor de implementat cu ajutorul unui calculator si un algoritm numit transformata Fourier, ceea ce vom incerca sa facem in continuare.
Exemplul semnalului dreptunghiular, simetric, cu amplitudinea de 1 V
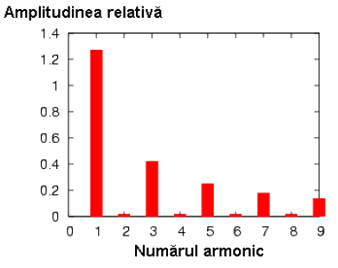
In graficul de mai jos, formele de unda sunt impartite in functie de frecventele lor sinusoidale, pana la armonica a 9-a. Amplitudinile armonicilor pare sunt aproximativ zero, iar a celor impare descresc de la 1 la 9 (prima este cea mai mare, ultima cea mai mica).
Bibliografie / Surse:
Tony R. Kuphaldt – Introducere in circuite electrice si electronice
Articolul de fata, face parte din varianta romaneasca a volumului de „Curent alternativ”, al doilea din seria lucrarilor „Lessons in Electric Circuits” scrise de Tony R. Kuphaldt.